해시 테이블 (Hash Table)
- 배경
- 직접 주소화 테이블 (Directed Address Table) 의 단점을 보완하기 위해
- 직접 주소화 테이블 (Directed Address Table)
- key, value를 저장할 때 key값으로 k를 갖는 원소는 index k에 저장하는 방식 (key를 그대로 인덱스로 쓰는 테이블)
- key가 적절(배열의 인덱스로 쓰기 적절)하면 상관이 없음 ex) (2,”노정호”), (1,”배준석”), (4,”정재헌”)
- 만약 (학번, 이름)이나 (아이디, 닉네임) 등의 key, value를 저장하는 상황에 문제가 발생
- (201622528, 박강욱) → 배열의 201622528 번째 공간에 value 저장 → 메모리 공간 낭비 발생
- (syunxttm, 박강욱) → 배열의 syunxttm 번째 공간은 없음 → key에 다양한 자료형을 담을 수 없음
- 이런 단점 (메모리 공간 낭비, 제한적인 key의 자료형)을 보완하기 위해 Hash Table 고안
- 개념
- (key, value) 데이터 쌍을 저장할 때 해시 함수 $h$ 를 이용해서 $h(k)$를 인덱스로 저장하는 자료구조
- 이때 “키 k값을 갖는 원소가 위치 $h(k)$에 해시된다”, “$h(k)$는 키 k의 해시값이다” 라고 표현
- key는 무조건 존재해야 하고, 중복되면 안됨 (해시 함수 $h$는 일대일 대응 함수)
- hash table을 구성하고 있는 (key, value) 데이터를 저장하는 각 공간을 slot 또는 bucket이라고 함
- 예시
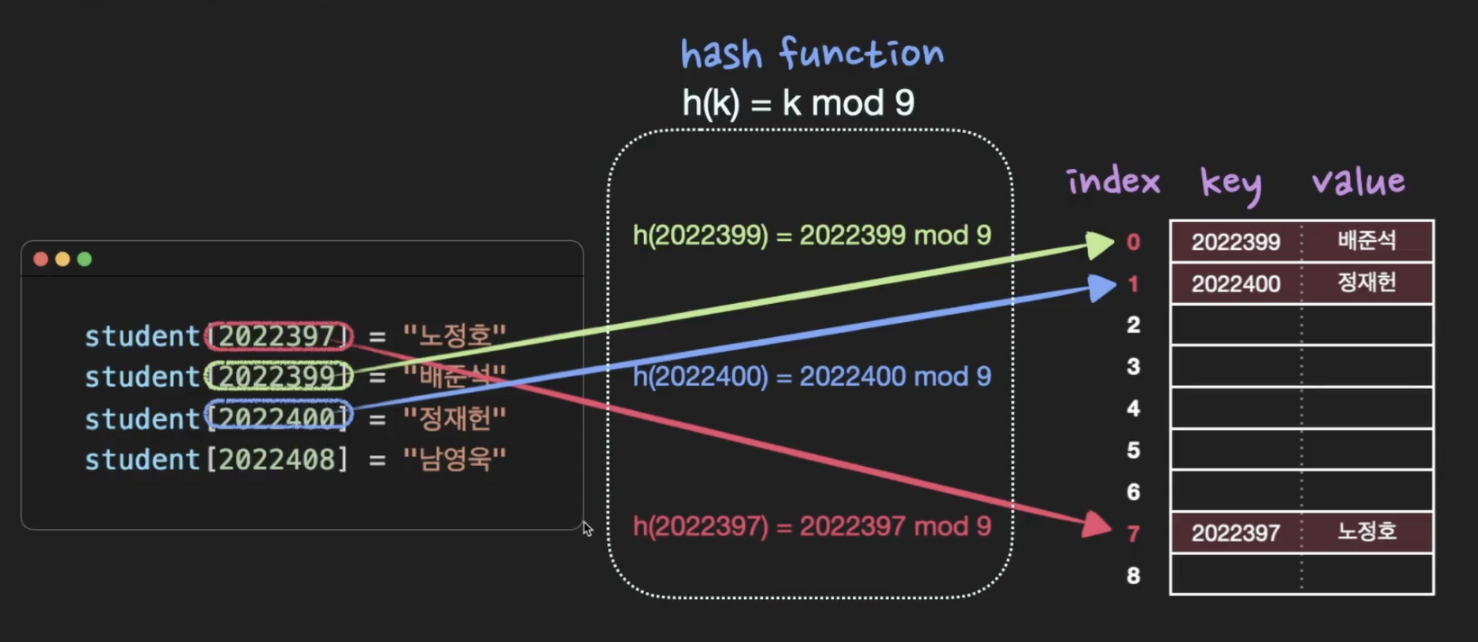
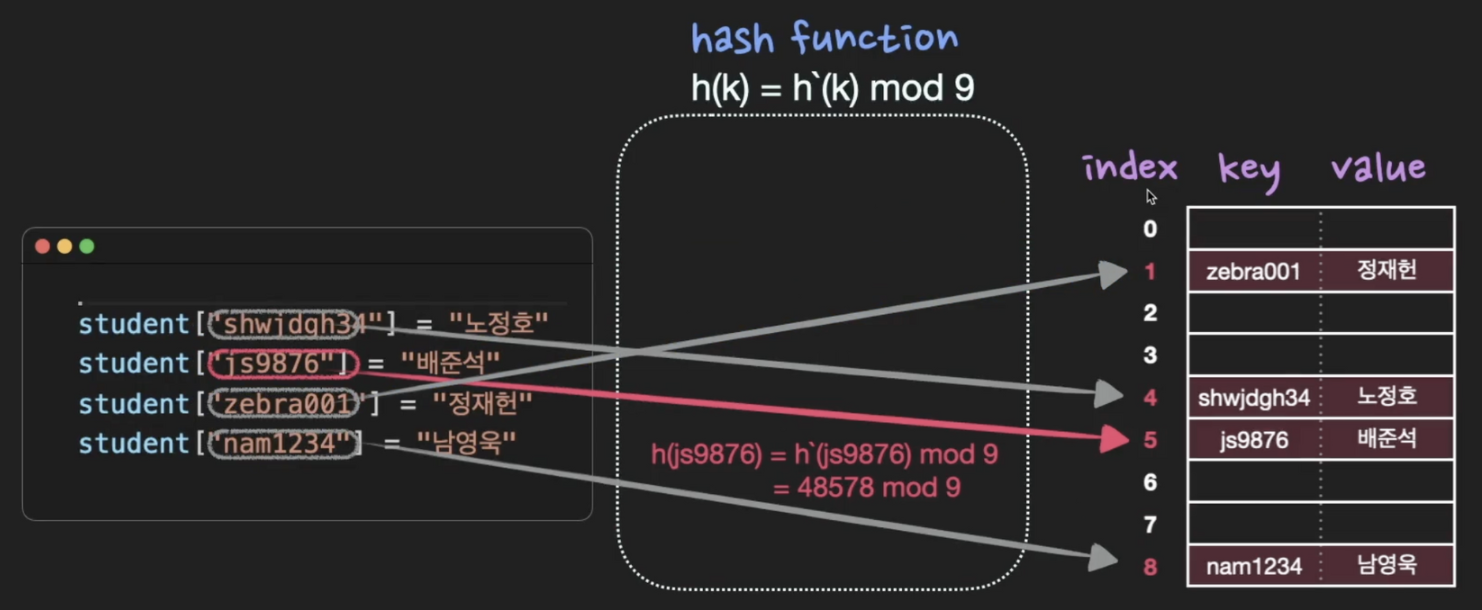
- Collision
- 해시값이 같은 경우 (index가 중복되는 경우) Collision이 발생함
- Collision을 해결하는 방법으로 Open Addressing, Chaining 등이 있음
- 좋은 해시 함수는 연산이 빠르면서 Collision이 잘 일어나지 않는 함수
- 시간복잡도 & 공간효율
- 저장, 검색, 삭제 모두 기본적으로 $O(1)$, collision의 경우 최악으로 $O(n)$
- 공간효율은 낮은 편 → slot 또는 bucket을 미리 확보해야 하기 때문
🔥 해시테이블 in 코딩 테스트
코딩 테스트 문제를 풀다 보면 해시테이블 개념을 자주 볼 수 있는데, 어떻게 써먹는 걸까?
해시테이블이 곧 딕셔너리다! 해시테이블은 key, value의 한 쌍을 해시 함수를 통해 저장할 수 있는 자료구조이다. 이를 딕셔너리 형태로 우리가 이용하는 것이다.
그렇다면, 딕셔너리는 어떤 상황에서 이점이 있을까?
해시테이블은 데이터 저장, 조회, 삭제 등의 시간복잡도가 O(1)이다. 이 말은, 무수히 많은 데이터를 저장하거나 데이터 탐색이 필요할 때 딕셔너리를 활용하면 시간복잡도를 엄청 줄일 수 있다!
개방 주소법 (Open Addressing) & 체이닝 (Chaining)
개방 주소법 (Open Addressing)
- 개념
- 미리 정한 규칙 (Linear, Quadratic, Double Hasing) 에 따라 해시 테이블 내에서 빈 슬롯을 찾는 방식
- 추가적인 메모리 사용하지 않음 → linked list 또는 tree를 통해 추가적인 메모리를 할당하는 chaining 방식에 비해 메모리 적게 사용
- 초기에 할당하는 메모리는 더 클 수도 있음
- 종류
- Linear Probing (선형 탐색) & Quadratic Probing (제곱 탐색)
- 충돌이 발생한 해시값으로부터 일정한 보폭 (+1, +2, +3 … / +1^2, +2^2, +3^2 …) 만큼 건너뛰면서 빈 슬롯을 찾는 방식
- 충돌이 많아지면 특정 영역에 데이터가 집중적으로 몰리는 클러스터링 현상 발생
- → 평균 탐색 시간 증가
- Double Hashing (이중 해시, 중복 해시)
- 충돌 발생 시 빈 슬롯을 찾기 위해 탐색하는 보폭을 또 하나의 해시 함수로부터 구하는 방식 (탐색 보폭을 결정하는 해시 함수를 하나 더 만듦)
- 기존 해시 함수 : 인덱스 구하기
- 추가된 해시 함수 : 탐색 보폭 구하기
- Linear Probing (선형 탐색) & Quadratic Probing (제곱 탐색)
체이닝 (Chaining)
- 개념
- linked list 또는 tree를 이용하여 collision을 해결하는 방식
- 해시값에 충돌이 발생하면, 해당 index에 노드를 하나 더 달아서 (key, value) 저장
- 시간복잡도
- 삽입 : O(1)
- 검색 : 기본적으로 O(1), worst case로 O(n)
- → 모든 해시값이 동일해서 하나의 index에만 모든 노드가 달린 경우
- 삭제 : 기본적으로 O(1), worst case로 O(n) (삭제하려면 검색을 해야 하므로 동일)
정리
해시 테이블, Hash Table
해시 테이블은 빠른 검색∙탐색을 위한 자료구조이며, key, value 쌍으로 데이터를 저장한다. 기본적으로 Array를 사용하여 저장하는데, 이는 Array의 검색 시간복잡도가 O(1)인 것의 이점(by random access) 을 활용하기 위함이다. (평균적으로 O(1), but 충돌 발생 시 worst case로 O(n))
큰 범위, 무작위 자료형의 key는 해시 함수를 통해 작은 범위, 정수형의 index로 해싱된다. (Array의 index로 활용해야 하므로 정수형 아닐까?)
해시 함수, Hash Function
해시를 논할 때 해시 함수는 꽤나 중요한 비중을 차지한다. 해시 함수의 성능이 해시 테이블의 효울과 직결되기 때문이다. 그렇다면, 해시 테이블을 잘 사용하기 위한 좋은 해시 함수는 어떤 함수를 말하는 걸까?
나는 그저 수학적으로 ‘일대일 대응 함수가 되게 설계하면 된다’고 생각했었는데, 이는 중요한 포인트가 아니었다. 아니, 당연하면서 제일 중요하고도 근본적인 방법 아닌가? CS적으로는 다르다. 실질적으로 생각해야 한다.
모든 값에 대한 일대일 대응 해시 함수를 설계한다는 것은 거의 불가능하기도 하고, 설령 그렇게 만든다고 해도 그건 Array와 다를 바 없기도 하고, 메모리를 너무 많이 차지하게 된다. 설계자 관점에서 집중해야 할 부분은 (1) 충돌을 최소화하면서, (2) 충돌에 대비한 대응 방법을 잘 설계하는 것이다.
충돌이 많아지면 시간복잡도가 점점 $O(1)$에서 $O(n)$이 되기 때문에 비효율적이다. 어설픈 해시 함수는 ‘빠른 탐색’이라는 해시의 소기 목적를 달성하지 못하게 만든다. 추가로, 좋은 해시 함수는 key의 일부분이 아닌 전체를 참조해서 만드는 함수이다.
충돌, Collisioin
충돌을 해결하는 방법으로는 여러가지가 있지만, 밑에서 얘기할 2가지의 기본적인 방법을 응용한 것들이다.
- 개방 주소법, Open Addressing
- 충돌이 발생하면 미리 정해진 규칙(Linear, Quadratic, Double Hashing)에 따라 비어있는 해시 버킷을 탐색하여 데이터를 저장하는 방식이다.
- Double Hashing은 탐색 보폭을 구하기 위해 또 하나의 해시 함수를 설계하여 사용하는 것이므로, Linear∙Quadratic보다 많은 연산량이 요구된다.
- 체이닝, Chaining
- 동일한 인덱스에 연결 리스트∙트리를 이어 붙여서 데이터를 저장하는 방식이다. 기본적으로 개방주소법보다 빠르다. 개방주소법은 충돌이 많아질 수록 클러스터링 현상(해시 테이블 밀도가 높아짐)에 의해 worst case 발생 빈도가 높아지기 때문이다. 분리연결법에서도 worst case가 발생할 수 있으나, *보조 해시 함수를 통해 조정할 수 있다.
- 분리연결법 구현 방식에는 연결 리스트 (Linked List)와 트리(Tree)가 있다. 각자 방식은 이름 그대로 해시 버킷에 각각의 자료구조를 연결하여 구현한 것이다. 연결 리스트는 데이터 추가, 삭제가 간단하지만 데이터가 많아질 수록 오버헤드∙메모리 사용량이 증가한다. 트리는 데이터가 적을 때 낭비되는 메모리 공간이 있지만, 많을 때는 연결 리스트보다 적다.
- 종합하자면, 트리는 기본적인 메모리 사용량이 많기 때문에 데이터가 적다면 연결 리스트를, 많다면 트리를 사용한다.
- 보조 해시 함수 : key값이 중복되지 않게 해시 함수 하나 더 쓰는 것을 말한다.
- 데이터 기준 : 해시 테이블의 한 버킷에 key∙value 쌍이 6개, 8개인지를 기준으로 삼는다. 6개 이하에서는 연결 리스트를, 7개가 된다면 여전히 연결 리스트를 유지하고, 8개를 넘어가는 상황에서부터 트리로 변경한다. 굳이 중간에 7을 남겨두는 이유는, 중간 여유를 두지 않을 시 연결 리스트 ↔ 트리 간의 switching cost가 증가하기 때문이다.
데이터의 개수가 적다면 개방 주소법이 더 효율적이다. worst case 발생 빈도도 적고 캐시 효율이 더 높기 때문이다. 하지만, 데이터의 개수가 많아진다면 개방 주소법은 해시 테이블을 확장해야 하기 때문에 작업이 많아진다. 분리 연결법을 사용한다면 테이블 확장을 보다 늦출 수 있기 때문에 더욱 유리하다.
해시 테이블을 확장하는 것을 해시 버킷 동적 확장(resize)라고 하는데, 해시 테이블이 가득 차기 전에 일정 개수 또는 비율 이상 채워지면 버킷의 개수를 두 배로 늘린다. 기준은 데이터가 전체 해시 버킷의 75% 이상이 될 때이고, 이때 0.75는 load factor라고도 불린다.
'CS > 자료구조' 카테고리의 다른 글
| [CS - 자료구조] 이진 탐색 트리 (BST, Binary Search Tree), Red-Black Tree (0) | 2023.03.29 |
|---|---|
| [CS - 자료구조] 트리 (Tree), 이진 트리 (Binary Tree) (0) | 2023.03.29 |
| [CS - 자료구조] 그래프 (Graph) (0) | 2023.03.29 |
| [CS - 자료구조] 큐 vs 스택 (Queue vs Stack) (0) | 2023.03.02 |
| [CS - 자료구조] 배열 & 연결 리스트 (Array & Linked List) (0) | 2023.01.19 |
![[CS - 자료구조] 해시 테이블 (Hash Table)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbAvkiz%2Fbtr6GVlyH1P%2FAAAAAAAAAAAAAAAAAAAAALS2cjhyWfHyxHm-IFl4wGCp5giH1knGkT5LowWD28pV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DfZOQe%252BFfwnsmoVIPwc%252FcWI%252BCpY0%253D)